Нормално разпределение

Статистиката превръща хаоса от числа в предвидими модели и ни позволява да правим изчисления за вероятности в почти всяка сфера – от медицината до финансите.

1. Нормалното разпределение: Природният стандарт

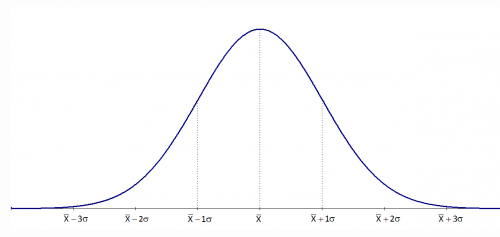
Представете си, че измерваме височината на 10 000 случайни хора. Повечето ще бъдат около средната височина. Малцина ще са много ниски и малцина – много високи. Ако начертаем това, получаваме Гаусова крива (камбановидна крива).

източник: spcforexcel , Dr. Bill McNeese

Основни характеристики:

Симетрия: Тя е идеално симетрична спрямо центъра.
Трите „М“ съвпадат: В перфектната крива $Средно = Медиана = Мода$ .
Асимптотичност: Краищата на кривата се доближават до оста, но теоретично никога не я докосват (винаги има минимален шанс за екстремно събитие).

2. Стандартно отклонение ( $\sigma$ )

Стандартното отклонение е статистически показател, който измерва колко „разпръснати“ са данните в една група спрямо тяхната средна стойност. Просто казано: то ни казва дали числата в един списък са близо едно до друго, или са разпръснати в широки граници.

Ниско стандартно отклонение: Означава, че повечето данни са много близо до средната стойност. Резултатите са предвидими и стабилни.
Високо стандартно отклонение: Означава, че данните са разпръснати далеч от средната стойност. Има голямо разнообразие или „шум“ в измерванията.

Представете си две групи от по петима души, които стрелят в мишена:

Група А: Всички стрелят много близо до центъра. Техните попадения имат ниско стандартно отклонение.
Група Б: Един удря центъра, друг е далеч вляво, трети – вдясно. Средно те също са „около центъра“, но техните попадения имат високо стандартно отклонение.

Математически стандартното отклонение се означава с гръцката буква сигма ( $\sigma$ ) за генерална съвкупност или с буквата $s$ за извадка.

Формулата за стандартно отклонение на извадка изглежда така:

s = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n - 1}}

Където:

$x_i$ : всяка отделна стойност от данните.
$\bar{x}$ : средната аритметична стойност.
$n$ : броят на стойностите в извадката.

Стандартното отклонение е полезно в много сфери:

Финанси: Използва се за измерване на риска. Високото отклонение при акциите означава висока волатилност (цената скача рязко нагоре и надолу).
Производство: Помага да се следи качеството. Ако частите, които произвеждате, имат голямо отклонение в размера, те няма да си пасват.
Метеорология: Помага да разберем колко устойчиви са температурите в даден регион.

Нека анализираме пример. Представете си, че имаме резултатите от тест на ученици (наричаме това извадка): Стойности ( $x$ ): 2,2,3,4,3,3,3,3,4,3, 5,6. След пресмятане разбираме, че стандартното отклонение на нашите данни е 1.24. Това означава, че средно резултатите на учениците се разминават със средното (3,42) с около 1.24 единици.

Това означава, че този клас е сплотен около центъра. Повечето ученици се движат около оценката „Среден (3)“.

Интересното тук е, че имаме струпване на много еднакви резултати (шест ученици имат оценка 3). Това прави групата много по-предвидима в средата си. Учителят може да заключи, че основната част от класа е усвоила съвсем базовите знания, но има трудности с по-сложния материал, който би ги извел към 5 или 6.

Ако изберете случаен ученик от тази група, е много вероятно (около 68% шанс) неговият резултат да бъде между 2.18 и 4.66 (това са $3.42 - 1.24$ и $3.42 + 1.24$ ).

Какво ни казва това? Почти всички ученици са в диапазона между „Слаб“ и „Добър“.
Сравнение: Ако отклонението беше още по-малко (например 0.5), почти целият клас щеше да има тройки. В нашия случай обаче, отклонението от 1.24 ни казва, че макар ядрото да е стабилно, все пак има „разсейване“ към по-високите и по-ниските оценки.

Аномалии: В тази група имаме резултати като 2 (два пъти) и 6 (веднъж).

Оценката 6 е на разстояние от $6 - 3.42 = 2.58$ единици от средното.
Това е повече от 2 стандартни отклонения ( $2 \times 1.24 = 2.48$ ).

Извод за учителя: Ученикът с оценка 6 е „изключение“ за този клас. Той се справя значително по-добре от останалите и стандартното отклонение ни помага да видим, че неговият резултат не е типичен. Учителят трябва да помисли за допълнителни задачи за този ученик, за да не му е скучно, докато останалите затвърждават материала за 3 и 4, както и за индивидуални задачи за учениците със слаби оценки.

Стандартното отклонение е най-полезно, когато сравняваме две (или повече) извадки:

Показател	Клас А (s=1.41)	Клас Б (s=0.5)
Среден успех	4.00	4.00
Равномерност	По-големи разлики между учениците.	Всички са почти на едно ниво.
Подход	Учителят трябва да обърне индивидуално внимание.	Учителят може да преподава на целия клас еднакво.

4. Извод за „екстремните“ случаи

В статистиката често се приема, че всичко, което е извън 2 стандартни отклонения, е необичайно.

Правилото 68-95-99.7

При данните, които следват т.нар. „нормално разпределение“ (камбановидна крива):

Около 68% от данните попадат в рамките на 1 стандартно отклонение от средното.
Около 95% попадат в рамките на 2 стандартни отклонения.
Около 99.7% попадат в рамките на 3 стандартни отклонения.

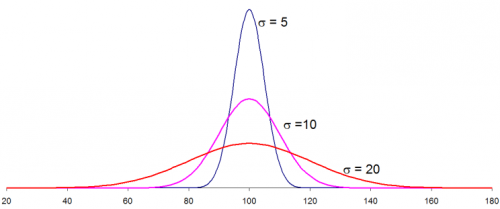
Стандартното отклонение не е просто число – то е мащабът на нашата крива. Ако $\sigma$ е малко, камбаната е висока и тесна (данните са еднакви). Ако $\sigma$ е голямо, камбаната е широка и разлята (голямо разнообразие).

източник: spcforexcel , Dr. Bill McNeese

3. Z-резултат: статистическа координата

Z-резултатът ни казва: „На колко стандартни отклонения от средното се намира дадена точка?“

Z-резултатът показва разстоянието на дадена стойност от средната аритметична стойност, измерено в единици стандартно отклонение. Той превръща суровите данни в число, което няма мерна единица.

z = \frac{x - \mu}{\sigma}

Ако $z = 0$ , точно в средата.
Ако $z = 2$ , по-високо/по-добре от 97.7% от другите.
Ако $z = -1.5$ , под средното.

Най-голямата сила на Z-резултата е, че ни позволява да сравняваме несравними неща.

Пример: Представете си, че искате да разберете в кой предмет сте по-добър спрямо класа си:

Математика: Имате 5.00 (Средно за класа 4.00, Станд. откл. 0.50)
Литература: Имате 5.50 (Средно за класа 5.00, Станд. откл. 1.00)

На пръв поглед оценката по Литература е по-висока. Но нека видим Z-резултатите:

Z по Математика: $(5.00 - 4.00) / 0.50 = \mathbf{+2.0}$
Z по Литература: $(5.50 - 5.00) / 1.00 = \mathbf{+0.5}$

Извод: Макар и с по-ниска оценка, по Математика вие сте „статистическа звезда“ (2 отклонения над другите), докато по Литература сте съвсем малко над средното.

Практическо приложение

Медицина: Педиатрите използват Z-резултати, за да проследят дали ръстът и теглото на бебето се развиват нормално спрямо връстниците му.
Финанси: Инвеститорите гледат Z-резултатите на акциите, за да разберат дали текущата цена е необичайно висока или ниска спрямо историята ѝ.
Контрол на качеството: Ако даден детайл в завода излезе със $Z > 3$ , машината веднага се спира, защото това е знак за повреда.

4. Квартили, Персентили и Аномалии

Стандартното отклонение и Z-резултатът разчитат на средната стойност, квартилите и персентилите се фокусират върху позицията на данните в един подреден списък. Докато медианата разделя данните на две, квартилите ги делят на четири (по 25%), а персентилите – на сто части.

източник: Wikimedia, Jeremy Kemp

Как намираме аномалии (Outliers)?

Аномалията е стойност, която е толкова отдалечена от останалите, че изглежда като грешка или извънредно събитие. Квартилите ни дават математически метод за тяхното откриване: Интерквартилния размах (IQR).

Намираме $IQR = Q_3 - Q_1$ .
Изчисляваме границите:
- Долна граница: $Q_1 - 1.5 \times IQR$
- Горна граница: $Q_3 + 1.5 \times IQR$
  
  Всичко извън тези „огради“ е статистическа аномалия.

Примери

Пример 1: Сравняване на резултати (Z-резултат)

Представете си фабрика, която пълни бутилки от 500 мл. Машините не са съвършени и винаги има малки вариации. След анализ на хиляди бутилки, фабриката установява следното:

Средно количество ( $\mu$ ): 500 мл
Стандартно отклонение ( $\sigma$ ): 2 мл

Да вземем три бутилки от поточната линия и да пресметнем техните „статистически координати“:

Бутилка А (498 мл):

$Z = \frac{498 - 500}{2} = \frac{-2}{2} = -1.0$
- Извод: Тази бутилка съдържа малко по-малко вода от средното, но е само на 1 стандартно отклонение разстояние. Това е напълно в рамките на нормалното за производствения процес.
Бутилка Б (501 мл):

$Z = \frac{501 - 500}{2} = \frac{1}{2} = +0.5$
- Извод: Тази бутилка е много близо до средното ниво. Тя е само на половин стандартно отклонение над центъра.
Бутилка В (507 мл):

$Z = \frac{507 - 500}{2} = \frac{7}{2} = +3.5$
- Извод: Тук имаме изключение. Z-резултат над 3.0 показва, че това събитие е изключително рядко (под 0.3% вероятност).

Чрез превръщането на милилитрите в Z-резултати, мениджърите могат да вземат решения без да гледат индивидуалните обеми:

Автоматизация: Софтуерът може да бъде настроен така, че ако види бутилка със Z < -2.5, тя автоматично да бъде отстранена от линията, защото е твърде празна и нарушава законите за защита на потребителите.
Диагностика: Ако средният Z-резултат на последните 100 бутилки започне да се измества към +1.5, това е ясен сигнал, че машината има нужда от калибриране, защото започва системно да препълва и фирмата губи пари.

Z-резултатът ни дава универсален език. Ако същата фирма има и завод за бутилки от 1.5 литра (където отклонението е по-голямо, например 10 мл), мениджърът може да попита: „Колко бутилки днес имаха $Z > 3$ ?“. Той не се интересува дали става дума за 507 мл или за 1540 мл – той търси статистическото отклонение от нормата.

Пример 2: Откриване на аномалии (IQR)

Представете си 11 продадени апартамента със следните цени (в хиляди евро):

70, 75, 80, 82, 85, 90, 92, 95, 100, 110, 250

Медиана ( $Q_2$ ): 90 (числото точно по средата).
Квартили:
- $Q_1$ (средата на долната половина) = 80.
- $Q_3$ (средата на горната половина) = 100.
Интерквартилен размах ( $IQR$ ): $100 - 80 = 20$ .
Проверка за аномалии:
- Горна граница: $100 + (1.5 \times 20) = 130$ .
- Резултат: Цената от 250 хил. е далеч над 130. Тя е статистическа аномалия. Може би това е луксозен пентхаус, докато останалите са стандартни жилища.

Въпроси

Основни:

Ако средният ръст е 170 см със $\sigma=5$ см, между кои две стойности попадат 95% от хората?
Какво ни казва 90-ият персентил за резултата на един кандидат-студент?
Защо при нормално разпределение медианата и средното са равни?
Наклонът на крива е статистически показател, който описва доколко едно разпределение е „изкривено“ спрямо центъра си. (Представете си, че хващате върха на камбаната и го дърпате наляво или надясно.) При положителна асиметрия (Right-skewed) Опашката на кривата е по-дълга от дясната страна, тоест Повечето данни са концентрирани вляво (малки стойности), но има няколко много големи стойности, които дърпат „опашката“ надясно. Нарисувайте примерна графика и дайте практически пример.
Ако Z-резултатът на даден човек е -3, как бихте го описали спрямо останалата популация?
Може ли стандартното отклонение да бъде отрицателно число? Обосновете се.
Как ще се промени Z-резултатът ви, ако стандартното отклонение на групата се увеличи, а вашият личен резултат остане същият?

Задачи

Даден е набор от данни със средно $\mu=50$ и $\sigma=8$ . Намерете Z-резултата за стойностите: а) 58, б) 42, в) 70.
В клас от 200 души, вие сте в 85-ия персентил. Колко души имат по-слаб резултат от вашия?
Пресметнете размаха и $IQR$ за данните: 5, 7, 8, 10, 12, 15, 20.
Инвестиционен анализ: Акция А има средна доходност 5% със $\sigma=1\%$ . Акция Б има средна доходност 7% със $\sigma=4\%$ . Коя акция бихте избрали, ако искате минимален риск (т.е. най-малка вероятност за големи загуби)? Обяснете чрез правилото 68-95-99.7.
Дизайн на врати: Средният ръст на мъжете е 175 см със $\sigma=10$ см. Колко висока трябва да е една врата, за да могат 97.7% от мъжете да преминават, без да се навеждат? (Подсказка: 97.7% съответства на $+2\sigma$ ).
Критично мислене: Имате данни за заплатите в софтуерна фирма. Повечето са между 3000 и 5000 лв., но трима мениджъри вземат по 50 000 лв. Ще бъде ли това нормално разпределение? Как ще изглежда графиката и кой показател (средно или медиана) ще бъде по-голям?
Допълнителни:

Логика и интуиция

Представи си две вериги кафенета – „Кафе А“ и „Кафе Б“.
- В „Кафе А“ средното време за приготвяне на кафе е 5 минути със стандартно отклонение 30 секунди.
- В „Кафе Б“ средното време е 5 минути със стандартно отклонение 3 минути.
Въпрос: В кое кафене е по-вероятно понякога да чакаш 10 минути за своето кафе и защо?

Работа с Z-резултат

Имаш двама кандидати за работа, които са държали различни тестове за интелигентност:
- Кандидат 1 има резултат 130 при среден за неговия тест 100 и стандартно отклонение 15.
- Кандидат 2 има резултат 140 при среден за неговия тест 120 и стандартно отклонение 20.
Въпрос: Кой от двамата се е справил по-добре спрямо своята група? (Използвай формулата $Z = (x - \mu) / \sigma$ )

Квартили и Аномалии

Имаш данни за заплатите в една малка фирма: 1200, 1300, 1400, 1500, 10 000 лв.
- Средната заплата е 3080 лв.
- Медианата ( $Q_2$ ) е 1400 лв.
Въпрос: Кой от двата показателя (средното или медианата) описва по-честно „нормалната“ заплата в тази фирма и как би нарекъл числото 10 000 в този контекст?