Математиката зад „Проклятието на измерението“ | от Maxime Wolf („Проклятието на измерението“ е термин, измислен от Ричард Белман) .
връзка
В областта на машинното обучение работата с вектори с висока размерност не е просто обичайна; това е от съществено значение. Това се илюстрира от архитектурата на популярни модели като Transformers. Например BERT използва 768-измерни вектори, за да кодира токените на входните последователности, които обработва, и за по-добро улавяне на сложни модели в данните. Като се има предвид, че нашият мозък се бори да визуализира всичко отвъд 3 измерения, използването на 768-измерни вектори е доста умопомрачително!
Въпреки че някои модели на машинно и задълбочено обучение се справят отлично в тези сценарии с голямо измерение, те също представляват много предизвикателства. В тази статия ще изследваме концепцията за „проклятието на размерността“, ще обясним някои интересни явления, свързани с нея, ще се задълбочим в математиката зад тези явления и ще обсъдим техните общи последици за вашите модели на машинно обучение.
Имайте предвид, че подробни математически доказателства, свързани с тази статия, са достъпни на моя уебсайт като допълнително разширение към тази статия.
Какво е проклятието на размерността?
Хората често приемат, че геометричните концепции, познати в три измерения, се държат по подобен начин в пространствата с по-високи измерения. Това не е така . С увеличаването на измерението възникват много интересни и неинтуитивни явления. „Проклятието на измерението“ е термин, изобретен от Ричард Белман (известен математик), който се отнася до всички тези изненадващи ефекти.
Това, което е толкова специално за високото измерение, е как „обемът“ на пространството (ще го изследваме по-подробно скоро) нараства експоненциално. Вземете градуирана линия (в едно измерение) от 1 до 10. На тази линия има 10 цели числа. Разширете това в 2 измерения: сега е квадрат с 10 × 10 = 100 точки с цели координати. Сега помислете за „само“ 80 измерения: вече ще имате 10⁸⁰ точки , което е броят на атомите във Вселената.
С други думи, с увеличаването на измерението, обемът на пространството нараства експоненциално, което води до все по-оскъдни данни.
Пространствата с големи размери са „празни“
Помислете за този друг пример. Искаме да изчислим най-отдалеченото разстояние между две точки в единичен хиперкуб (където всяка страна има дължина 1):
В 1 измерение (хиперкубът е линеен сегмент от 0 до 1), максималното разстояние е просто 1.
В 2 измерения (хиперкубът образува квадрат), максималното разстояние е разстоянието между противоположните ъгли [0,0] и [1,1], което е √2, изчислено с помощта на Питагоровата теорема.
Разширявайки тази концепция до n измерения , разстоянието между точките при [0,0,…,0] и [1,1,…,1] е √n. Тази формула възниква, защото всяко допълнително измерение добавя квадрат от 1 към сумата под квадратния корен (отново по Питагоровата теорема).
Интересното е, че с нарастването на броя на измеренията n,
най-голямото разстояние в рамките на хиперкуба нараства със скорост O(√n). Това явление илюстрира ефекта на намаляваща възвращаемост , където увеличенията в пространственото пространство водят до пропорционално по-малки печалби в пространственото разстояние. Повече подробности за този ефект и неговите последици ще бъдат разгледани в следващите раздели на тази статия.
Понятието разстояние във високи измерения
Нека се потопим по-дълбоко в понятието разстояния, което започнахме да изследваме в предишния раздел.
Имахме първия си поглед върху това как пространствата с високи измерения правят понятието разстояние почти безсмислено . Но какво всъщност означава това и можем ли математически да визуализираме този феномен?
Нека разгледаме експеримент, използвайки същия n-измерен единичен хиперкуб, който дефинирахме преди. Първо, ние генерираме набор от данни чрез произволно вземане на проби от много точки в този куб: ние ефективно симулираме многовариантно равномерно разпределение. След това вземаме проба от друга точка (точка на „заявка“) от това разпределение и наблюдаваме разстоянието от най-близкия и най-далечния съсед в нашия набор от данни .
Ето съответния код на Python.
def generate_data(dimension, num_points):
“’ Generate random data points within [0, 1] for each coordinate in the given dimension “’
data = np.random.rand(num_points, dimension)
return data
def neighbors(data, query_point):
“’ Returns the nearest and farthest point in data from query_point “’ nearest_distance = float(‘inf’)
farthest_distance = 0
for point in data:
distance = np.linalg.norm(point – query_point)
if distance < nearest_distance:
nearest_distance = distance
if distance > farthest_distance:
farthest_distance = distance
return nearest_distance, farthest_distance
Можем също да начертаем тези разстояния (изображения в оригиналната статия). Използвайки логаритмична скала, наблюдаваме, че относителната разлика между разстоянието до най-близкия и най-далечния съсед има тенденция да намалява с увеличаване на измерението.
Това е много неинтуитивно поведение: както беше обяснено в предишния раздел, точките са много раздалечени една от друга поради
експоненциално нарастващия обем на пространството, но в същото време относителните разстояния между точките стават по-малки.
Идеята за най-близките съседи изчезва
Това означава, че самата концепция за разстояние става по-малко уместна и по-малко дискриминираща с увеличаването на размерите на пространството. Както можете да си представите, това създава проблеми за алгоритмите за машинно обучение, които разчитат единствено на разстояния като kNN.
Математиката: n-топката
Сега ще говорим за някои други интересни явления. За това ще ни трябва n-топката . N-топката е обобщение на топка в n измерения. N-топката с радиус R е съвкупността от точки на разстояние най-много R от центъра на пространството 0.
Нека разгледаме радиус от 1. Топката 1 е отсечката [-1, 1]. 2-топката е дискът, ограничен от единичната окръжност, чието уравнение е x² + y² ≤ 1. 3-топката (това, което обикновено наричаме „топка“) има уравнението x² + y² + z² ≤ 1. Както разбирате , можем да разширим тази дефиниция до всяко измерение:
Въпросът сега е: какъв е обемът на тази топка? Това не е лесен въпрос и изисква доста математика, която няма да описвам тук. Въпреки това можете да намерите всички подробности на моя уебсайт, в публикацията ми за обема на n-ball .
След много забавление (интегрално смятане) можете да докажете, че обемът на n-топката може да бъде изразен по следния начин, където Γ означава гама функцията.
Например, с R = 1 и n = 2, обемът е πR², тъй като Γ(2) = 1. Това наистина е „обемът“ на 2-топката (наричан също „площ“ на кръг в този случай ).
Въпреки това, освен че е интересно математическо предизвикателство, обемът на n-топката има и някои много изненадващи свойства.
С увеличаването на измерението n обемът на n-топката се сближава до 0.
Това е вярно за всеки радиус, но нека визуализираме това явление с няколко стойности на R.
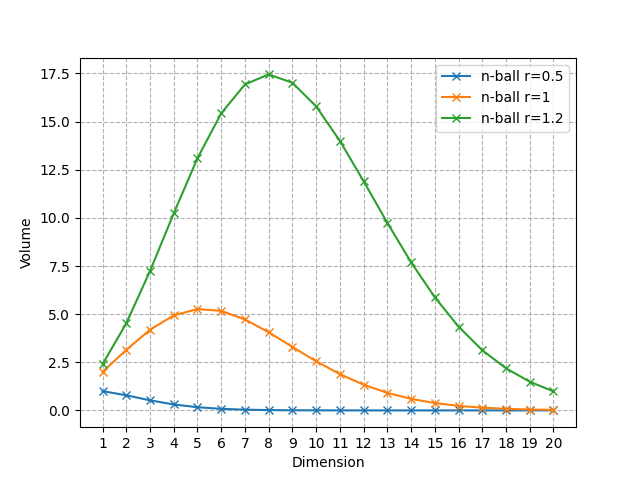
Обем на n-топката за различни радиуси с увеличаване на измерението (Изображение от автора)
Както можете да видите, тя се сближава само до 0, но започва с увеличаване и след това намалява до 0. За R = 1 топката с най-голям обем е топката 5 и стойността на n, която достига максимума, се измества към надясно, когато R се увеличава.
Ето първите стойности на обема на единичната n-топка, до n = 10.

Обем на единицата n-топка за различни стойности на n (Изображение от автора)
Обемът на единична топка с големи размери е концентриран близо до нейната повърхност.
За малки размери обемът на топката изглежда доста „хомогенен“: това не е така при големите размери.
Сферична черупка
Нека разгледаме n-топка с радиус R и друга с радиус R-dR, където dR е много малко. Частта от n-топката между тези 2 топки се нарича „черупка“ и съответства на частта от топката близо до нейната повърхност (вижте визуализацията по-горе в 3D). Можем да изчислим съотношението между „вътрешния“ обем на топката и обема само на тънката обвивка.
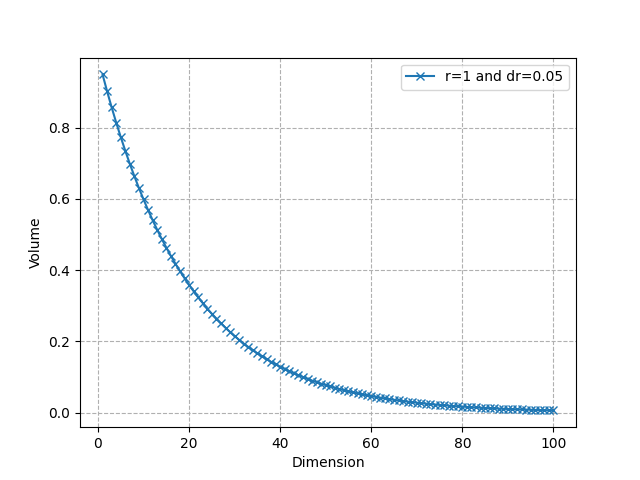
Съотношение (вътрешен обем / общ обем) с увеличаване на n (Изображение от автора)
Както виждаме, той се сближава много бързо до 0: почти целият обем е близо до повърхността в пространства с големи размери. Например, за R = 1, dR = 0,05 и n = 50, около 92,3% от обема е концентриран в тънката обвивка. Това показва, че в по-високите измерения обемът е в „ъглите“. Това отново е свързано с изкривяването на концепцията за разстояние, което видяхме по-рано.
Обърнете внимание, че обемът на единичния хиперкуб (тук обозначаващ куб с център нула и дължина на страната 2) е 2ⁿ. Единичната сфера е основно „празна“ в много високи измерения, докато единичният хиперкуб, напротив, получава експоненциално повече точки. Отново това показва как идеята за „най-близкия съсед“ на точка губи своята ефективност, защото почти няма точка на разстояние R от точка на заявка q, когато n е голямо.
Проклятие на размерите, пренастройването и бръснача на Окам
Проклятието на размерността е тясно свързано с принципа на
пренастройване. Поради експоненциалното нарастване на обема на пространството с измерението, ние се нуждаем от много големи набори от данни за адекватно улавяне и моделиране на високоизмерни модели. Още по-лошо: имаме нужда от брой проби, които растат експоненциално с измерението, за да преодолеем това ограничение. Този сценарий, характеризиращ се с много функции, но относително малко точки от данни, е особено предразположен към пренастройване .
Бръсначът на Окам предполага, че по-простите модели обикновено са по-добри от сложните, тъй като е по-малко вероятно да прекалят. Този принцип е особено уместен в контексти с високи измерения (където проклятието на размерността играе роля), тъй като насърчава
намаляването на сложността на модела.
Прилагането на принципа на бръснача на Окам в сценарии с големи размери може да означава намаляване на размерността на самия проблем (чрез методи като PCA, избор на характеристики и т.н.), като по този начин смекчава някои ефекти от проклятието на размерността . Опростяването на структурата на модела или пространството на функциите помага за управлението на разпределението на оскъдни данни и за превръщането на показателите за разстояние отново по-смислени. Например намаляването на размерността е много често срещана
предварителна стъпка преди прилагането на алгоритъма kNN. По-нови методи, като ANN (приблизителни най-близки съседи), също се появяват като начин за справяне със сценарии с голямо измерение.
Въпреки че очертахме предизвикателствата на високоразмерните настройки в машинното обучение, има и някои предимства !
Високите измерения могат да подобрят линейната разделимост , правейки техники като методите на ядрото по-ефективни.
Освен това, архитектурите за дълбоко обучение са особено умели в навигирането и извличането на сложни модели от пространства с големи размери.
Както винаги при машинното обучение, това е компромис : използването на тези предимства включва балансиране на увеличените изчислителни изисквания с потенциални печалби в производителността на модела.
Заключение
Надяваме се, че това ви дава представа колко „странна“ може да бъде геометрията във високо измерение и многото предизвикателства, които поставя пред разработването на модел за машинно обучение. Видяхме как в пространства с големи размери данните са много оскъдни, но също така са склонни да бъдат концентрирани в ъглите и разстоянията губят своята полезност. За по-задълбочено гмуркане в n-ball и математическите доказателства, препоръчвам ви да посетите разширението на тази статия на моя уебсайт .
Въпреки че „проклятието на размерността“ очертава значителни ограничения в пространствата с високи размери, вълнуващо е да видим как съвременните модели на дълбоко обучение са все по-умели в навигирането в тези сложности. Помислете за моделите за вграждане или най-новите LLM, например, които използват вектори с много големи размери за по-ефективно разпознаване и моделиране на текстови модели.
