Ирански математик превръща уравненията в зашеметяващо изкуство.
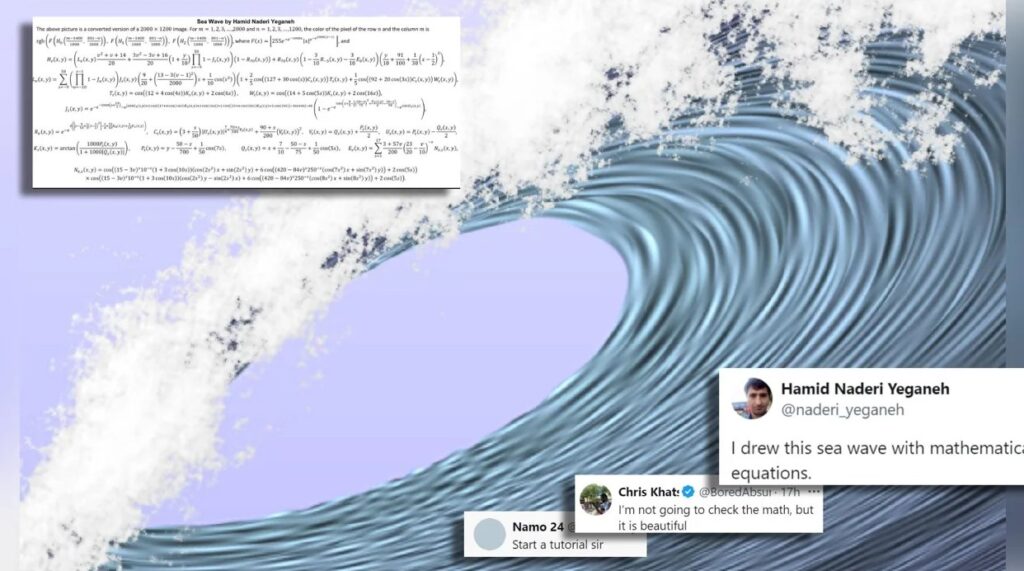
Красиво творчество на иранския математик Хамид Надер Йеганех, който създава спиращи дъха произведения на изкуството, използвайки математически формули. Неговите творби изглеждат изненадващо простички – сякаш са създадени с персонализирана четка за Photoshop или са генерирани от някаква програма. В действителност обаче, Хамид е успял да изобрази разбиваща се морска вълна само с уравнения.
Заплетените математически илюстрации на Хамид включват експоненциални функции, тригонометрични функции, вълнови функции, последователността на Фибоначи и други. Някои от неговите творби са били използвани за корици на световноизвестни списания, като например неговата „9000 затъмнения“ , която краси корицата на броя от ноември 2017 г. на Scientific American.
Хамид е завършил бакалавърска степен по математика в университета в Ком и магистратура в Технологичния университет „Шариф“. Той е и носител на златен медал от 38-ото издание на Състезанието на Иранското математическо общество. Една от неговите творби, „Птица в полет“ , е съставена от 20 001 кръга! „Фрактална Африка“ пък е изградена от безкраен брой осмоъгълници, наподобяващи формата на Африканския континент.
Самият Хамид споделя, че създава тези оптически математически произведения на изкуството, като пуска програмата си на операционна система Linux.
Неговите творби предизвикват истински фурор в интернет. Те сякаш дават отговор на вечната детска дилема: „За какво ще ми трябват някога тези тригонометрии, геометрии и други сложни глупости?“ (Разбира се, освен очевидното им приложение в науките и технологиите в ежедневието).
Творчеството на Хамид показва красотата и неочакваните приложения на математиката, излизайки извън рамките на традиционната представа за нея като наука, полезна само за „науките и технологиите“.
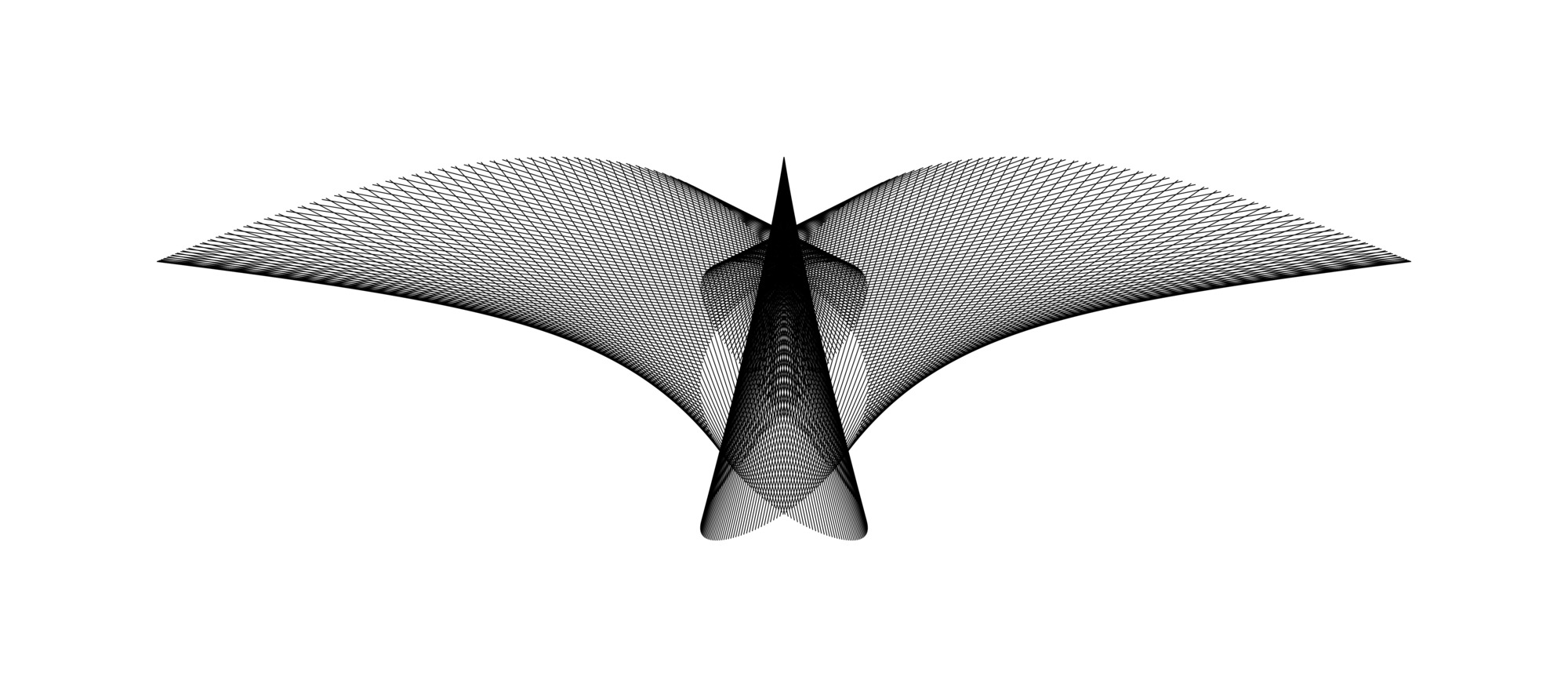
Горното изображение се описва така:
За всяко 𝑖=1,2,3,…,500 крайнитете точки 𝑖 на линиите са:
(32(sin(2𝜋𝑖500+𝜋3))7,14(cos(6𝜋𝑖500))2)
and
(15sin(6𝜋𝑖500+𝜋5),−23(sin(2𝜋𝑖500−𝜋3))2).
Вижте повече в неговия профил в инстаграм.



