Подготовка за Олимпиада – Областен кръг - Школа по математика София-Мат

Числови изрази и свойства на числата

1. задача от 2010 г., зад. 1 (Числови изрази и неизвестни числа)

а) Пресметнете израза: $(118 178 : 74 + 8403) : 5 + 10$ . б) Намерете неизвестното число $x$ от равенството: $(239 138 : x) \cdot 6 + 612 = 2010$ .
В1: Намерете разликата $A - B$ , ако $A = (305 \cdot 204 - 60 000) : 100 + 999$ , а $B$ е неизвестното число в равенството $(B : 25 + 1024) \cdot 2 - 2048 = 2024$ .
В2: Пресметнете стойността на $M = (123 \cdot 321 - 39 000) : 9 + (2025 : 5 - 400)$ . Намерете $y$ , ако е вярно, че $(M + y) : 11 - 100 = 50$ .
В3: Дадени са изразите $P = (55 555 : 11 + 45) : 50$ и $Q = (1000 - 888) \cdot 5$ . Намерете числото $X$ , за което е вярно, че $(X - P) \cdot 3 + Q = 2026$ .
В4: Намерете неизвестното число $x$, ако е вярно равенството:$((x : 15 + 240) \cdot 6 – 800) : 10 = 100$.
След като намерите $x$, пресметнете стойността на израза $A = (x \cdot 2 – 150) : 5 + 2026$.
В5: Пресметнете по най-рационален начин сбора на следната числова редица:$S = (1 + 3 + 5 + 7 + \dots + 99) – (2 + 4 + 6 + 8 + \dots + 98)$.
Колко е разликата между получената сума и числото, което е 5 пъти по-малко от 255?
В6: Дадени са три числа. Първото е най-малкото четирицифрено число, записано с различни четни цифри. Второто е равно на $(2025 : 9 + 75) \cdot 4$ . Третото число е неизвестното $z$ в уравнението $(z - 1200) \cdot 3 = 1800$ . Подредете числата по големина и намерете техния сбор.
В4: Намерете числото $x$ , за което е вярно: $(2025 - (x \cdot 5 + 150)) : 10 + 88 = 103$ . След като намерите $x$ , пресметнете стойността на израза $A = (x + 125) \cdot 8 - 2000$ .
В5: Дадени са две числа. Първото е неизвестното $y$ от равенството $(y : 4 + 1024) \cdot 2 - 2000 = 48$ . Второто е стойността на израза $M = 123 \cdot 9 - 111 \cdot 8$ . Намерете с колко първото число е по-голямо от второто.
В6: Пресметнете израза $P = 1000 - 990 + 980 - 970 + \dots + 20 - 10$ . Към получената стойност добавете неизвестното число $z$ от равенството $(z - P) : 5 + 120 = 200$ .

2. задача от 2014 г., зад. 1 (Парични пресмятания)

Разполагам с $15 \cdot 2014 - 10 \cdot 2013 + 11 \cdot 2012 - 11 \cdot 2011 - 7 \cdot 1313$ евро (е.). Ще ми стигнат ли да купя общо $528 : (72 \cdot 18 - 46 \cdot 23 + 36 \cdot 9 - 23 \cdot 23)$ енциклопедии, които струват по $(17 \cdot 3200 - 33 \cdot 1600) : (73 \cdot 4 - 53 \cdot 4)$ е. всяка? Колко е. ще останат или не достигат?
В1: Един антиквар разполага със сума $S = 25 \cdot 2025 - 24 \cdot 2024 + 10 \cdot 100 - 2000$ евро (е.). Той иска да купи серия от редки монети. Всяка монета струва $M = (15 \cdot 450 - 30 \cdot 200) : (50 - 25)$ е. Колко монети може да купи и колко е. ще му останат за витрина, която струва $V = 1234 - 111 \cdot 11$ е.?
В2: Сравнете стойностите на двата портфейла: $A = (2024 \cdot 15 - 2023 \cdot 14) : 13$ евро (е.) и $B = (15 \cdot 15 \cdot 15 - 10 \cdot 10 \cdot 10) : 5$ е. С колко е. $A$ е по-голям или по-малък от $B?$ .
В3: Намерете цената на училищно оборудване, ако един таблет струва $(99 \cdot 99 + 99) : 100$ евро (е.), а един проектор е 5 пъти по-скъп от таблета. Ще стигнат ли 2000 е. за закупуването на 15 таблета и 2 проектора?

Геометрия

1. задача от 2010 г., зад. 2 (Правоъгълник, разделен на квадрати)

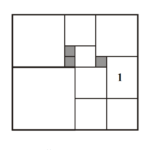
Начертайте голям правоъгълник. Той е разделен на 12 части: 11 квадрата и един малък правоъгълник (означен с 1). Всяко от сивите квадратчета има страна 1см. Намерете лицето на големия правоъгълник.

В2: Фигура е съставена от 5 квадрата, подредени във формата на главна буква „L“ (три вертикални и два хоризонтални). Периметърът на цялата фигура е 144 см. Намерете лицето на един от тези квадрати.
В3: Квадрат със страна 24 см е разделен на два еднакви правоъгълника. Единият от тях е разделен на три еднакви по-малки квадрата. Намерете лицето на един от тези малки квадрати и обиколката на правоъгълника, който остава неразрязан.
В4: Правоъгълник е съставен от три еднакви квадрата, долепени един до друг в редица. Обиколката на целия правоъгълник е 64 см. Намерете лицето му в квадратни сантиметри. Ако всеки от трите квадрата се раздели на четири нови еднакви по-малки квадратчета, колко ще бъде обиколката на едно такова малко квадратче?
В5: Даден е квадрат със страна 18 см. Той е разделен на два правоъгълника така, че обиколката на единия е с 12 см по-голяма от обиколката на другия. Намерете размерите (дължина и ширина) и лицето на по-малкия правоъгълник.
В6: Три еднакви квадрата са подредени един върху друг, за да образуват вертикална колона (правоъгълник). Обиколката на тази колона е 80 см. Към нея отдясно се долепя четвърти квадрат, чиято страна е равна на дължината на цялата колона. Намерете обиколката и лицето на новополучената фигура.

2. задача от 2012 г., зад. 4.2 (Правоъгълник от шест квадрата)

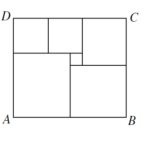
Правоъгълник $ABCD$ е запълнен от шест квадрата. Намерете обиколката на $ABCD$ , ако дължината на страната $AB = 546$ см.

В2: Начертайте квадрат $ABCD$ . От него е отрязан по-малък квадрат от единия ъгъл. Получената нова фигура (с 6 страни) има обиколка 80 см. Ако страната на отрязания малък квадрат е 5 см, колко сантиметра е била страната на първоначалния голям квадрат?
В4: Квадрат е разделен на два правоъгълника чрез линия, успоредна на една от неговите страни. Обиколката на първия правоъгълник е 50 см, а обиколката на втория е 70 см. Намерете страната на първоначалния квадрат и неговото лице в квадратни сантиметри.

В5: Правоъгълник е съставен от три еднакви квадрата, които са подредени един до друг в хоризонтална редица. Ако обиколката на целия правоъгълник е 96 см, намерете лицето на един от тези квадрати. Как ще се промени общата обиколка, ако добавим още два такива квадрата към редицата?

В6: Имаме четири еднакви правоъгълника, всеки с дължина 12 см и ширина 3 см. Те са подредени така, че да образуват нов голям правоъгълник с възможно най-голяма обиколка (без да се застъпват). Намерете обиколката и лицето на получената голяма фигура. Опишете как трябва да бъдат долепени правоъгълниците, за да се получи този резултат.

Текстови и логически задачи

1. задача от 2004 г., зад. 4.1 (Магазинът за тетрадки)

В магазин докарали 180 тетрадки (с широки редове и на квадратчета). През първия ден продали 36 с редове и 24 на квадратчета. Останалите с редове били 3 пъти повече от тези на квадратчета. По колко тетрадки от всеки вид са били доставени първоначално?
В1: В библиотека има 500 книги – романи и учебници. След като заделили 50 романа и 70 учебника за дарение, останалите романи станали точно 4 пъти повече от останалите учебници. Колко книги от всеки вид е имало в библиотеката в самото начало?
В2: В две каси има общо 1000 евро (е.). От първата похарчили 150 е., а във втората добавили 50 е. Сега в първата каса има 2 пъти по-малко пари, отколкото във втората. Колко е. е имало във всяка каса в началото?
В4: В една каса има общо 45 евро (е.). Парите са в монети от по 2 е. и банкноти от по 5 е. Ако общият брой на монетите и банкнотите е 15, намерете колко евроцента (е.ц.) общо струват всички монети от 2 е. в касата.
В5: Майстор боядисва 4 еднакви стаи за 6 часа и 40 минути. Неговият чирак боядисва същата стая за 2 часа и 30 минути. Ако двамата започнат да работят заедно в 08:30 часа сутринта, в колко часа ще са приключили с боядисването на точно 3 такива стаи?
В6: Един автомат за кафе приема монети от 20 евроцента (е.ц.), 50 е.ц. и 1 евро (е.). Чаша кафе струва 80 е.ц. Димитър пуснал точно 3 монети и автоматът му върнал 40 е.ц. ресто. Намерете всички възможни комбинации от монети, които Димитър може да е пуснал. Колко е.ц. е най-малката сума, която може да се получи от останалите му монети, ако в джоба си е имал общо 5 монети по 50 е.ц. и 2 монети по 1 е.?

2. задача от 2008 г., зад. 3 (Сладкарят и тортите)

За направата на 5 големи и 7 малки торти на сладкар са нужни 4 ч. и 36 мин. Голяма торта се прави за 12 мин. повече от малка. За колко време ще се направят 4 големи и 2 малки торти?
В1: Един майстор изработва 3 маси и 5 стола за общо 19 часа. Ако за изработката на една маса са нужни 3 часа повече работа, отколкото за един стол, за колко време майсторът ще направи пълен комплект от 1 маса и 4 стола?
В2: Робот боядисва 10 големи и 5 малки стени за 105 минути. Времето за боядисване на голяма стена е два пъти повече от това за малка. Колко стени общо (равен брой големи и малки) може да боядиса роботът за точно 2 часа?

3. задача от 2018 г., зад. 4.3 (Монетите на Диана)

Диана има монети от 1 евро (е.) (7 г), 50 евроцента (е.ц.) (4 г), 20 е.ц. (3 г) и 10 е.ц. (2 г). Тя купува 3 горещи шоколада по 30 е.ц. всеки. За всеки шоколад тя плаща с точно 2 различни монети. Намерете общото тегло на използваните монети.
В1: Касиер разполага с монети от 2 евро (е.) (9 г), 1 е. (7 г) и 50 евроцента (е.ц.) (4 г). Клиент трябва да плати точно 5 е., като използва общо 4 монети. Какво е възможното общо тегло на тези монети?
В2: Имате везна и монети от 10, 20 и 50 евроцента (е.ц.). Теглата им са съответно 2 г, 3 г и 4 г. Ако имате купчина монети със сума точно 2 евро (е.) и общо тегло 22 грама, колко монети от 50 е.ц. има в купчината?
В3: В автомат за играчки се пускат жетони от 50 евроцента (е.ц.) и 1 евро (е.). Жетоните от 50 е.ц. тежат 5 г, а тези от 1 е. тежат 8 г. В края на деня в автомата има общо 50 е. с общо тегло 460 грама. Колко играчки са купени, ако една играчка струва 1 е. и 50 е.ц.?
В4: Плик с шоколадови бонбони тежи 450 грама и струва 3 евро (е.) и 60 евроцента (е.ц.). Известно е, че 100 грама от бонбоните струват точно 80 е.ц. Намерете колко е. и колко е.ц. ще струват 2 кг от същите бонбони и какво ще бъде теглото на празната опаковка (плика).

В5: В една игрална зала се използват жетони от 50 евроцента (е.ц.) и 1 евро (е.). Жетонът от 50 е.ц. тежи 7 грама, а този от 1 е. тежи 10 грама. Мартин има в джоба си общо 15 монети, които тежат точно 126 грама. Колко е. общо има Мартин и колко от монетите му са от по 50 е.ц.?

4. задача (Движение)

В1: Влак с дължина 150 метра преминава през тунел с дължина 450 метра за точно 30 секунди. Намерете скоростта на влака в метри за секунда. Колко секунди ще са му нужни, за да премине покрай стълб, ако се движи със същата скорост?
В2: На всеки 10 минути от автогарата тръгва автобус, който се движи със скорост 60 км/ч. Лек автомобил тръгва едновременно с първия автобус, но се движи със 90 км/ч. След колко минути автомобилът ще бъде на разстояние 15 км пред първия автобус и на колко км ще се намира от втория автобус в този момент?
В3: Велосипедист изминава разстоянието между два града за 4 часа. Ако увеличи скоростта си с 5 км/ч, ще измине същото разстояние за 3 часа. Намерете разстоянието между градовете и първоначалната скорост на велосипедиста.
В4: От два града, разстоянието между които е 360 км, тръгнали едновременно един срещу друг два автомобила. Скоростта на първия е 80 км/ч, а на втория е 100 км/ч. След колко часа разстоянието между тях ще бъде точно 90 км, преди да са се срещнали?
В5: Велосипедист се движи със скорост 12 км/ч. Един час след него от същия пункт и в същата посока тръгва мотоциклетист със скорост 36 км/ч. След колко минути мотоциклетистът ще настигне велосипедиста?
В6: Двама бегачи стартират едновременно от една и съща точка на кръгова пътека с дължина 400 метра. Ако се движат в една и съща посока със скорости 5 м/сек и 3 м/сек, след колко секунди по-бързият бегач ще застигне по-бавния за първи път?