Продължете към съдържанието

Уравнения на окръжност, елипса, хипербола, парабола

Наричат се криви от втори ред (или криви от втора степен), защото общото им уравнение е полином от втора степен спрямо променливите $x$ и $y$. Всяка крива от втори ред (елипса, хипербола, парабола, окръжност и двойка прави*) може да бъде описана с едно общо уравнение в декартова координатна система:

$$Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0$$

Където $A, B, C, D, E, F$ са константи, и поне една от константите $A, B, C$ е различна от нула, за да имаме именно уравнение от втора степен.

Наричаме ги и конични сечения, защото визуално се получават при пресичане на кръгов конус с равнина.

1. Окръжност – Канонично уравнение и пресечни точки с права

Канонично уравнение на окръжност

Окръжността е множеството от всички точки в равнината, които са на едно и също разстояние $r$ (радиус) от дадена фиксирана точка $C(x_0, y_0)$ (център).

Каноничното (нормалното, стандартно) уравнение на окръжност с център $C(x_0, y_0)$ и радиус $r$ е:

$$(x – x_0)^2 + (y – y_0)^2 = r^2$$
  • Специален случай: Ако центърът е в началото на координатната система $O(0, 0)$, уравнението става:
    $$x^2 + y^2 = r^2$$

Пресечни точки с права

За да намерите пресечните точки между една окръжност и една права, трябва да решите система от двете уравнения.

  1. Уравнение на окръжността: $(x – x_0)^2 + (y – y_0)^2 = r^2$

  2. Уравнение на правата: Правата обикновено се дава в явен вид $y = mx + n$ или в общ вид $Ax + By + C = 0$.

Метод:

  • Изразявате едната променлива (например $y$) от уравнението на правата.

  • Замествате този израз в уравнението на окръжността.

  • Получавате квадратно уравнение относно другата променлива (в случая $x$).

Брой на пресечните точки: Броят на реалните решения на квадратното уравнение ($D$) определя колко пресечни точки има:

  • Ако $D > 0$: Две пресечни точки (правата е секуща).

  • Ако $D = 0$: Една пресечна точка (правата е допирателна).

  • Ако $D < 0$: Няма пресечни точки.

2. Елипса, Хипербола, Парабола

Елипса

Елипсата е множеството от точки, за които сумата от разстоянията до две фиксирани точки (фокуси $F_1$ и $F_2$) е постоянна ($2a$).

Канонично уравнение

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
Елемент Описание
$a$ Голяма полуос
$b$ Малка полуос
$2a$ Голяма ос (дължината ѝ)
$2b$ Малка ос (дължината ѝ)
$c$ Фокално разстояние ($c = \sqrt{a^2 – b^2}$)
$F_1, F_2$ Фокуси ($(\pm c, 0)$)
$e$ Ексцентрицитет ($e = c/a$, $0 < e < 1$)
Върхове $(\pm a, 0)$ и $(0, \pm b)$

източник: https://byjus.com/maths/ellipse/

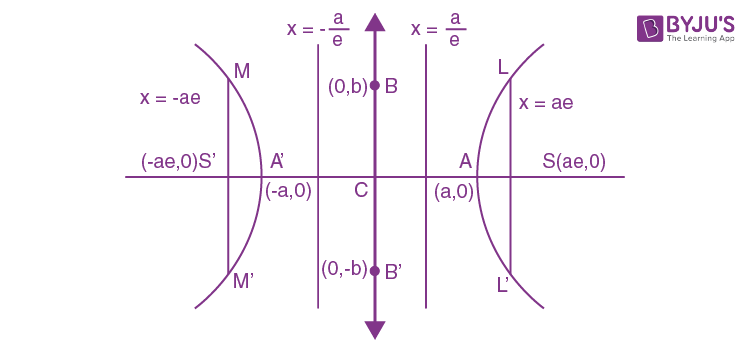
Хипербола

Хиперболата е множеството от точки, за които абсолютната стойност на разликата от разстоянията до две фиксирани точки (фокуси $F_1$ и $F_2$) е постоянна ($2a$).

Канонично уравнение

$$\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$$
Елемент Описание
$a$ Реална полуос
$b$ Имагинерна полуос
$2a$ Реална ос (дължината ѝ)
$c$ Фокално разстояние ($c = \sqrt{a^2 + b^2}$)
$F_1, F_2$ Фокуси ($(\pm c, 0)$)
$e$ Ексцентрицитет ($e = c/a$, $e > 1$)
Върхове $(\pm a, 0)$
Асимптоти Правата $y = \pm \frac{b}{a} x$

източник: https://byjus.com/maths/ellipse/

Парабола

Параболата е множеството от точки, които са равноотдалечени от една фиксирана точка (фокус $F$) и една фиксирана права (директриса $d$).

Канонично уравнение

В зависимост от ориентацията, има четири основни канонични уравнения. Най-често срещаното (отворена надясно) е:

$$y^2 = 2px$$
Елемент Описание
$p$ Фокален параметър (разстояние от фокуса до директрисата)
$F$ Фокус ($(p/2, 0)$)
$d$ Директриса (правата $x = -p/2$)
Връх Началото на координатната система $(0, 0)$
Ос на симетрия Оста $Ox$

източник: https://byjus.com/maths/standard-equations-of-parabola/

  • Други ориентации:

    • $y^2 = -2px$: Отворена наляво.

    • $x^2 = 2py$: Отворена нагоре (типична за графиката на $f(x) = ax^2$).

    • $x^2 = -2py$: Отворена надолу.

3. Бележки

Двойка прави може да бъде записана като произведение на две линейни уравнения, равно на нула. Например, двете прави $L_1: a_1x + b_1y + c_1 = 0$ и $L_2: a_2x + b_2y + c_2 = 0$ имат общо уравнение:

$$(a_1x + b_1y + c_1)(a_2x + b_2y + c_2) = 0$$

Когато разкрием скобите, това уравнение също приема формата на общото уравнение на крива от втори ред.

Двойка прави попада в категорията на т.нар. разпадащи се (дегенерирани) конични сечения.

Примерни задачи:

1. Окръжност и права: Пресечни точки

Дадена е окръжността с уравнение $x^2 + y^2 = 25$ и правата с уравнение $y = x + 1$. Намерете пресечните им точки.

  1. Записваме системата:
    $$\begin{cases} x^2 + y^2 = 25 \\ y = x + 1 \end{cases}$$
  2. Заместваме $y$ от второто уравнение в първото:
    $$x^2 + (x + 1)^2 = 25$$
  3. Разкриваме скобите и опростяваме:
    $$x^2 + (x^2 + 2x + 1) = 25$$
    $$2x^2 + 2x + 1 – 25 = 0$$
    $$2x^2 + 2x – 24 = 0$$
  4. Делим на 2 и решаваме квадратното уравнение:
    $$x^2 + x – 12 = 0$$

    Използваме формулата за корените или намираме с Виет:

    • $D = 1^2 – 4(1)(-12) = 1 + 48 = 49$

    • $x_{1,2} = \frac{-1 \pm \sqrt{49}}{2} = \frac{-1 \pm 7}{2}$
      $$x_1 = \frac{6}{2} = 3$$
      $$x_2 = \frac{-8}{2} = -4$$

  5. Намираме съответните стойности на $y$ от $y = x + 1$:

    • За $x_1 = 3$: $y_1 = 3 + 1 = 4$

    • За $x_2 = -4$: $y_2 = -4 + 1 = -3$

Пресечните точки са $A(3, 4)$ и $B(-4, -3)$.

2. Елипса: Определяне на елементи

Дадено е уравнението на елипсата $4x^2 + 9y^2 = 36$. Намерете дължините на осите, координатите на фокуситe и ексцентрицитета.

  1. Привеждаме уравнението в каноничен вид $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$:
    $$4x^2 + 9y^2 = 36$$

    Разделяме цялото уравнение на 36:

    $$\frac{4x^2}{36} + \frac{9y^2}{36} = \frac{36}{36}$$
    $$\frac{x^2}{9} + \frac{y^2}{4} = 1$$

  2. Намираме $a^2$ и $b^2$:

    • $a^2 = 9 \implies \mathbf{a = 3}$ (голяма полуос)

    • $b^2 = 4 \implies \mathbf{b = 2}$ (малка полуос)

  3. Дължини на осите:

    • Голяма ос ($2a$): $2 \cdot 3 = \mathbf{6}$

    • Малка ос ($2b$): $2 \cdot 2 = \mathbf{4}$

  4. Намираме фокалното разстояние $c$ от $c^2 = a^2 – b^2$:
    $$c^2 = 9 – 4 = 5$$
    $$\mathbf{c = \sqrt{5}}$$
  5. Координати на фокуситe $F(\pm c, 0)$:
    $$F_1(-\sqrt{5}, 0) \quad \text{и} \quad F_2(\sqrt{5}, 0)$$
  6. Намираме ексцентрицитета $e = c/a$:
    $$e = \frac{\sqrt{5}}{3}$$

3. Хипербола: определяне на асимптоти

Дадено е уравнението на хиперболата $x^2 – 16y^2 = 16$. Намерете уравненията на нейните асимптоти.

  1. Привеждаме уравнението в каноничен вид $\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$:
    $$x^2 – 16y^2 = 16$$

    Разделяме цялото уравнение на 16:

    $$\frac{x^2}{16} – \frac{16y^2}{16} = \frac{16}{16}$$
    $$\frac{x^2}{16} – \frac{y^2}{1} = 1$$

  2. Намираме $a^2$ и $b^2$:

    • $a^2 = 16 \implies \mathbf{a = 4}$

    • $b^2 = 1 \implies \mathbf{b = 1}$

  3. Уравненията на асимптотите са $y = \pm \frac{b}{a} x$:
    $$y = \pm \frac{1}{4} x$$

Уравненията на асимптотите са $y = \frac{1}{4} x$ и $y = -\frac{1}{4} x$.

4. Парабола: Намиране на фокус и директриса

Дадено е уравнението на параболата $y^2 = 10x$. Намерете координатите на фокуса и уравнението на директрисата.

  1. Сравняваме с каноничния вид $y^2 = 2px$:
    $$2p = 10$$
  2. Намираме фокалния параметър $p$:
    $$\mathbf{p = 5}$$
  3. Координати на фокуса $F(p/2, 0)$:
    $$F(\frac{5}{2}, 0) \quad \text{или} \quad \mathbf{F(2.5, 0)}$$
  4. Уравнение на директрисата $x = -p/2$:
    $$x = -\frac{5}{2} \quad \text{или} \quad \mathbf{x = -2.5}$$

Но защо?

Ето за какво е нужна тази теория, разделено по основни направления:

1. Научни приложения

    • Астрономия и Орбитална механика: Това е може би най-известното и класическо приложение.

      • Елипса: Орбитите на всички планети, комети и повечето изкуствени спътници около Слънцето или Земята са елипси (според законите на Кеплер).

    • Оптика и акустика: Коничните сечения имат уникални отражателни свойства, които се използват в дизайна на огледала и антени.

      • Парабола: Всички лъчи, идващи успоредно на оста на параболата, се фокусират в една точка (фокус). Това е принципът на параболичните антени (сателитни чинии, радиотелескопи) и фаровете на автомобилите.

2. Технологични приложения

  • Строителство и архитектура:

    • Парабола: Параболата е най-здравата форма за арки и мостове, тъй като силите на тежестта се разпределят равномерно. Използва се в дизайна на много известни мостове и куполи.

    • Окръжност: Основа на всяко кръгово и цилиндрично съоръжение, тръба, колело или зъбно колело.

  • Компютърна графика и игри: Уравненията на кривите от втори ред са основни за бързото и точно изобразяване на:

    • Кръгли форми, дъги и цилиндри в 3D моделирането.

    • Траектории на снаряди, топки и други обекти в симулации и видеоигри.

  • Дизайн на машини:

    • Формата на зъбните колела често се описва с параболични или хиперболични криви за оптимално предаване на движение.

Основни задачи за конични сечения

1. Окръжност: стандартно уравнение

Намерете каноничното уравнение на окръжност с център $C(-3, 4)$ и радиус $r = 5$.

2. Окръжност: общо към канонично

Дадено е общото уравнение на окръжността $x^2 + y^2 – 6x + 2y – 6 = 0$. Определете координатите на нейния център $C(x_0, y_0)$ и радиуса $r$.

3. Окръжност и права: пресечни точки

Намерете пресечните точки между окръжността $x^2 + y^2 = 13$ и правата $3x – 2y – 6 = 0$.

4. Елипса: канонично уравнение

Дадена е елипса, чиито фокуси са $F_1(-4, 0)$ и $F_2(4, 0)$, а голямата ѝ полуос е $a = 5$. Намерете каноничното уравнение на елипсата.

5. Елипса: елементи по уравнение

За елипсата с уравнение $25x^2 + 9y^2 = 225$, определете:

  • Дължините на полуосите $a$ и $b$.

  • Координатите на фокусите $F_1$ и $F_2$.

  • Ексцентрицитета $e$.

6. Хипербола: фокално разстояние

Дадена е хиперболата $\frac{x^2}{36} – \frac{y^2}{64} = 1$. Намерете фокалното разстояние $c$ и координатите на върховете.

7. Хипербола: уравнения на асимптотите

Намерете уравненията на асимптотите на хиперболата с уравнение $16x^2 – 9y^2 = 144$.

8. Парабола: фокус и директриса

Намерете координатите на фокуса $F$ и уравнението на директрисата $d$ за параболата $y^2 = 8x$.

9. Парабола: уравнение по фокус

Параболата има връх в началото на координатната система $O(0, 0)$ и фокус $F(0, 3)$. Намерете нейното канонично уравнение.

10. Обща задача: идентифициране

Определете каква крива от втори ред е представена от всяко от следните уравнения и дайте името ѝ:

  • a) $9x^2 – 4y^2 = 36$

  • b) $4x^2 + 4y^2 = 16$

  • c) $x^2 + 2y^2 = 18$

  • d) $y^2 = -4x$

10 Интересни интегрирани задачи

1. Допирателна и Перпендикуляр

Намерете уравнението на допирателната към окръжността $x^2 + y^2 = 25$ в точката $P(3, -4)$. След това намерете уравнението на права, която е перпендикулярна на тази допирателна и минава през центъра на окръжността.

2. Елипса и Ъглов Коефициент

Елипса е дадена с уравнението $\frac{x^2}{10} + \frac{y^2}{4} = 1$. През фокуса $F_1$ прекарайте права с ъглов коефициент $k=1$. Намерете уравнението на тази права и проверете дали пресича елипсата.

3. Хипербола и Ъгъл между Прави

Хипербола е дадена с уравнението $4x^2 – 5y^2 = 20$. Намерете уравненията на нейните асимптоти и изчислете ъгъла $\theta$ между тях. (Можете да използвате формулата $\tan(\theta) = \left|\frac{k_2 – k_1}{1 + k_1 k_2}\right|$).

4. Парабола и Успоредна Права

Дадена е параболата $y^2 = 12x$. Намерете уравнението на допирателната към параболата, която е успоредна на правата $2x – y + 5 = 0$.

5. Окръжност по Три Условия (Геометрично Място)

Намерете уравнението на окръжност, която:

  1. Има център $C(x_0, y_0)$ върху правата $y = x + 1$.

  2. Минава през началото на координатната система $O(0, 0)$.

  3. Радиусът й е $r = 5$.

6. Елипса и Перпендикулярни Диаметри

Намерете уравнението на елипса, ако разстоянието между фокусите е $2c = 6$, а нейните директриси са перпендикулярни на правата $x – 5 = 0$. (Директрисите са $x = \pm a^2/c$).

7. Хипербола и Допиране

Дадена е правата $y = 2x + n$. Намерете стойността на $n$, при която тази права е допирателна към хиперболата $4x^2 – y^2 = 12$. (Може да се използва условието за допиране на права $y=kx+n$ към хипербола $\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1$, което е $n^2 = a^2k^2 – b^2$).

8. Парабола: Фокус, Директриса и Ъгъл

Параболата има фокус $F(2, 0)$ и директриса $x = -2$.

  1. Намерете каноничното уравнение на параболата.

  2. Намерете ъгъла, който сключва с оста $Ox$ отсечката, свързваща фокуса $F$ с точка $P(8, 8)$ от параболата.

9. Две Прави и Окръжност (Взаимно Положение)

Определете взаимното положение на правите $L_1: 2x – 3y + 6 = 0$ и $L_2: 3x + 2y – 1 = 0$. След това намерете уравнението на окръжността, която има за диаметър отсечката между пресечната точка на $L_1$ и $L_2$ и точката $A(1, 1)$.

10. Елипса с успоредни допирателни

Намерете уравненията на двете допирателни към елипсата $x^2 + 4y^2 = 8$, които са успоредни на правата $x + 2y – 1 = 0$.

 

© София-Мат ЕООД

 

 

 

 

 

 

Facebook
X (Twitter)
Copy link
URL has been copied successfully!