Продължете към съдържанието

Обратна пропорция / пропорционалност

    Обратната пропорционалност не е просто формула в учебника – тя е законът на „баланса“. Ако имаш фиксирано количество от нещо (пари, време, храна), колкото на повече части го делиш, толкова по-малко остава за всяка част. Ако едно нещо расте, другото задължително намалява, за да остане светът в равновесие.

    Представете си, че сте поръчали една огромна фамилна пица. Тя е нашият Коефициент ($k$) – той е фиксиран, не се променя.

    1. Променливите ($x$ и $y$): Ако $x$ е броят на приятелите ви, а $y$ е размерът на парчето за всеки, вижте какво става:

      • Ако дойде повече народ ($x$ расте), парчетата стават по-малки ($y$ намалява).

      • Ако сте само двама ($x$ намалява), ще се пръснете от ядене ($y$ расте)!

    1. Какво трябва да знаем?

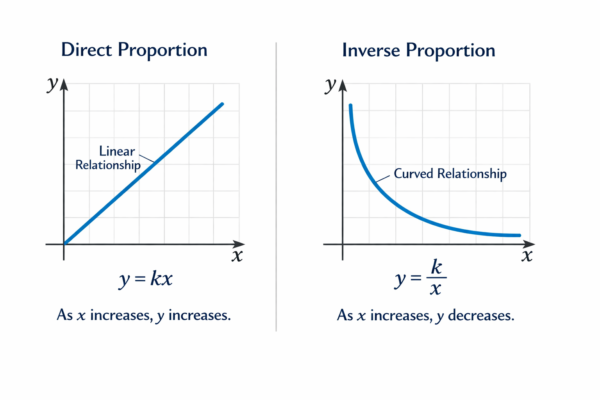
    Дефиниция: Две величини са обратно пропорционални, ако при увеличаването на едната няколко пъти, другата се намалява същия брой пъти.

    • Формула: $y = \frac{k}{x}$ или $x \cdot y = k$

    • Коефициент ($k$): Това е постоянно число ($k \neq 0$). То показва произведението на двете променливи. Ако знаеш една двойка стойности $(x, y)$, винаги можеш да намериш $k$, като ги умножиш.

    • Графика: Нарича се хипербола и е вид крива. Тя никога не докосва осите и има симетрия.

    • MгBeast Мисия: Имаш $1200 000,00$ € бюджет за награди в Giveaway. Колкото повече победители избереш ($x$), толкова по-малка сума пари ще получи всеки ($y$).

    • DJ Парти: Имаш списък с песни за точно 2 часа ($k$). Ако увеличиш темпото (BPM) и песните станат по-кратки, ще трябва да пуснеш много повече песни, за да запълниш времето.

    • Строеж в Minecraft: Трябва да изкопаеш дупка от 1000 блока. Ако поканиш 10 приятели, ще си готов за 1 час. Ако копаеш сам, ще ти трябват 10 часа. Повече копачи = по-малко време!

    2. Основни задачи

    Цел: Усвояване на формулата и работа с коефициента.

    Колона А Колона Б
    1. Намери $y$, ако $k = 24$ и $x = 8$. 2. Намери $k$, ако $x = 0,5$ и $y = 40,00$ €.
    3. Ако $x \cdot y = 100$, колко е $y$ при $x = 2,5$? 4. При $k = 15$, пресметни $x$, ако $y = 0,3$.
    5. Цената на сок е $1,20$ € за 200 грама. Колко литра купуваш с $6,00$ €? 6. Точка $B(4; 1,5)$ лежи ли на $y = \frac{6}{x}$?
    7. Ако $x$ се увеличи 5 пъти, какво става с $y$? 8. Намери $k$ за хипербола през $M(10; 0,2)$.
    9. Попълни: $y = \frac{k}{x}$ преминава през $(2; 12,50$ €$)$. 10. Пресметни $y$ при $x = 0,1$ и $k = 7$.
    11. Ако $y=2$ при $x=5$, намери $y$ при $x=10$. 12. Колко е $k$, ако $x$ и $y$ са „половинки“ ($0,5$)?
    13. Намери $k$ от таблица: $x=1, y=20; x=2, y=10$. 14. Може ли $y = 0$ да е в обратна пропорционалност?
    15. Намери $y$, ако $k = -12$ и $x = 4$. 16. Пресметни $x$ при $y = 0,01$ и $k = 1$.
    17. Трима работници чистят двор за 4 ч. Колко часа отнема на един? 18. Ако $k=0,75$, намери $y$ при $x=0,25$.
    19. Правоъгълник има $S=50$ см$^2$. Намери $b$, ако $a=12,5$ см. 20. Как се променя $y$, ако $x$ се намали 10 пъти?
    21. Превърни $y = \frac{4}{0,5x}$ в стандартен вид $y = \frac{k}{x}$. 22. Намери $k$ от таблица: $(2; 15), (5; 6), (10; 3)$.
    23. Ако $y = \frac{100}{x}$, намери $y$ за $x = 40$. 24. Колко струва 1 кг захар, ако $5$ кг са $6,25$ €?
    25. Намери $x$, ако $y = 250$ и $k = 25$. 26. В кои квадранти е $y = \frac{5}{x}$?
    27. Ако за $12,00$ € купуваш 8 тетрадки, колко е $k$ (обща сума)? 28. Начертай графика на $y = \frac{1}{x}$ за $x=1, 2, 4$.
    29. Намери $y$, ако $k = \frac{1}{2}$ и $x = 2$. 30. Провери: $3 \cdot 4 = 2 \cdot 6$. Обратно проп. ли са?

    3. По-трудни задачи

    Цел: Логическо мислене и текстови казуси.

    1. Кола изминава разстояние за 3 ч. със $100,0$ км/ч. С колко трябва да увеличи скоростта си, за да стигне за 2,5 ч.?

    2. Кораб изминава разстояние при $v=30$ възла за 12 ч. За колко часа ще го измине при $v=40$?

    3. Правоъгълник има площ $36$ см$^2$. Изразете страната $a$ чрез $b$ и начертайте примерна таблица.

    4. Петима бояджии боядисват сграда за 8 дни. Колко дни ще са нужни на 10 бояджии?

    5. Намери пресечната точка на $y = \frac{16}{x}$ и правата $y = x$.

    6. Ако $k$ се увеличи двойно, как се променя графиката?

    7. Имаш 200 г разтвор с 15% концентрация. Колко вода трябва да добавиш, за да стане 5%? (Масата на веществото $k$ е константа)

    8. Газ в цилиндър заема $2$ л при налягане $1,5$ атм. Какво е налягането при обем $0,5$ л? ($P \cdot V = const$)

    9. Намери $k$, ако $y(x+2) = 10$ при $x=3$.

    10. Графиката на обр. пропорц. минава през $M(0,5; 12)$. Намери стойноста на $y$ при $x=3$.

    11. Намери пресечните точки на $y = \frac{8}{x}$ и $y = 0,5x$.

    12. Магазин намалява цената на стока с 20%. С колко процента трябва да се увеличи обемът на продажбите, за да остане оборотът ($k$) същият?

    13. При каква стойност на $a$ точката $A(a; a)$ лежи на $y = \frac{16}{x}$?

    14. Два зъбни колела са зацепени. Първото има 20 зъба и прави 60 оборота. Второто има 30 зъба – колко оборота прави?

    15. Напишете уравнението на хипербола, минаваща през $P(2,5; 4)$.

    16. Как се променя $k$, ако увеличим и $x$, и $y$ два пъти?

    17. Една чешма пълни басейн за 12 ч. За колко време ще го напълнят 3 чешми?

    18. Ако $x+y=10$ и $x, y$ са обратно пропорционални с $k=9$, намери $x$ и $y$.

    19. Кола пътува от А до Б със скорост $v$. Ако увеличи скоростта си с 25%, с колко процента ще намалее времето за пътуване?

    20. Начертайте графиките на $y = \frac{4}{x}$ и $y = -\frac{4}{x}$ в една координатна система.

    4. Предизвикателни задачи

    Цел: Математическо майсторство.

    1. Дадена е функцията $f(x) = \frac{k}{x}$. Ако $f(2) + f(4) = 6,00$, намери $k$.

    2. Три числа са обратно пропорционални на 2, 3 и 6. Сумата им е 36,00. Намери числата.

    3. Намери лицето на триъгълника, образуван от допирателната към $y = \frac{1}{x}$ в точка $(1;1)$ и координатните оси.

    4. Точките $A(1; y_1)$ и $B(x_2; 4)$ лежат на $y = \frac{8}{x}$. Намери дължината на отсечката $AB$.

    5. Ако $y = \frac{k}{x}$, покажи че $\frac{y_1}{y_2} = \frac{x_2}{x_1}$.

    6. В кои квадранти лежи графиката, ако $k < 0$?

    7. Решете уравнението $\frac{12}{x} = x + 1$.

    8. Група приятели наемат вила за 240,00 €. Ако дойдат още двама, всеки ще плати с 20,00 € по-малко. Колко са били първоначално?

    9. Изразете зависимостта между съпротивление ($R$) и сила на тока ($I$) при постоянно напрежение $U = 220,00$ V.

    10. Намерете параметъра $m$, за който точката $P(m; m+2)$ лежи на графиката $y = \frac{8}{x}$.

    © София-Мат ЕООД

     

     

     

     

    Facebook
    X (Twitter)
    Copy link
    URL has been copied successfully!